
Or, looked at another way, for every LFSR implementation, the characteristic polynomial can be written in terms of two primitive polynomials,įor every primitive polynomial there are four linear feedback shift registers (LFSRs). This means that there are two possible LFSR implementations for every The reciprocal of a primitive polynomial,įor example, by taking the reciprocal of the primitive polynomial Is zero, there is no feedback connection and no XOR gate in that position. Is 1, then we include a feedback connection and an XOR gate in that position. Shows how the feedback taps on a LFSR correspond to the nonzero coefficients of the primitive polynomial. Lists the one with the fewest nonzero coefficients. There are many primitive polynomials for each There is no easy way to determine the coefficients of primitive polynomials, especially for large This corresponds to the primitive polynomial = 0, 1, 3 and thus the nonzero coefficients are A schematic for a type 1 LFSR is shown.Īny primitive polynomial can be written as Primitive polynomial coefficients for LFSRs (linear feedback shift registers) that generate a maximal-length PRBS (pseudorandom binary sequence). Nevertheless signature analysis with high error-coverage rates is found to produce high fault coverage. The problem lies in our assumption that all bad-circuit bit-streams are equally likely, and this is not true in practice (for example, bit-stream outputs of all ones or all zeros are more likely to occur as a result of faults). Unfortunately, these equations for error coverage are rather meaningless since there is no easy way to relate the error coverage to fault coverage. This is a very high probability of error and we would not use such a short test sequence and such a short signature register in practice. In general, if the length of the test sequence isĪnd the length of the signature register is If all bad circuit bit-streams are equally likely (and this is a poor assumption) then 0.118 is also the probability of aliasing. Since there are a total of 128 – 1 = 127 bit-streams due to bad circuits, the fraction of bad-circuit bit-streams that cause aliasing is 15 / 127, or 0.118. Thus there are 128 / 8 or 16 bit-streams that produce the good signature, one of these belongs to the good circuit, the remaining 15 cause aliasing. It turns out that this is a good assumption. We assume that each of these 128 bit-stream patterns is equally likely to produce any of the eight (all-zeros is an allowed pattern in a signature register) possible 3-bit signatures. Or 128 possible 7-bit-long bit-stream patterns. , the bit stream input to the signature analysis register is 7 bits long. There is a small probability that the signature of a bad circuit will be the same as a good circuit. The good and bad circuits produced different signatures. The bad circuit signature, '000', differs from the good circuit and the signature can either be compared with the known good signature on-chip or the signature may be shifted out and compared off-chip (both approaches are used in practice). Shows the waveforms in the good and bad circuit. The signature is formed as R0R1R2 seven clock edges (on the eighth clock cycle) after the active-low reset is taken high.

(b) shows how the bit sequences are calculated in the good circuit. (a) shows the bit sequences in the circuit, both for a good circuit and for a bad circuit with a stuck-at-1 fault, F1.

LFSR1 is initialized to '100' (Q0 = 1, Q1 = 0, Q2 = 0) and LFSR2 is initialized to '000'.
LFSR2 computes the signature ('011' for the good circuit) of the CUT.

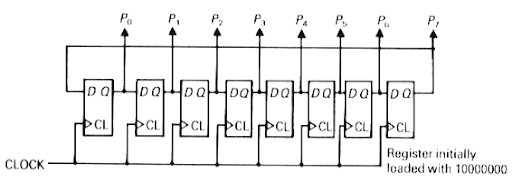
To form the simple BIST structure shown in The signature, Q1Q2Q3, is formed from shift-and-add operations on the sequence of input bits (IN). The LFSR is initialized to Q1Q2Q3 = '000' using the common RES (reset) signal. Hewlett-Packard to test equipment in the field in the late 1970s.Ī 3-bit serial-input signature register (SISR) using an LFSR (linear feedback shift register). This causes the signature to change from a known good value and we shall then know that the circuit under test is bad. If the input sequence comes from logic that we wish to test, a fault in the logic will cause the input sequence to change. ) are long enough, it is unlikely (though possible) that two different input sequences will produce the same signature. At the end of the input sequence the shift-register contents, With an additional XOR gate used in the first stage of the shift register.


 0 kommentar(er)
0 kommentar(er)
